JAX Featured

Optimizers in JAX and Flax

Derrick Mwiti

Aug 21, 2022 • 7 min read

Optimizers are applied when training neural networks to reduce the error between the true and predicted values. This optimization is done via gradient descent. Gradient descent adjusts errors in the network through a cost function. In JAX, optimizers are applied from the Optax library.

Optimizers can be classified into two broad categories:

Adaptive such as Adam, Adagrad, AdaDelta, and RMSProp.
Accelerated stochastic gradient descent (SGD), for example, SGD with momentum, heavy-ball method (HB), and Nesterov accelerated gradient (NAG).

Let's look at common optimizer functions used in JAX and Flax.

Adaptive vs stochastic gradient descent (SGD) optimizers

When performing optimization, adaptive optimizers start with large update steps but reduce the step size as they get close to the global minimum. This ensures that they don't miss the global minimum.

Adaptive optimizers such as Adam are quite common because they converge faster, but they may have poor generalization.

SGD-based optimizers apply a global learning rate on all parameters, while adaptive optimizers calculate a learning rate for each parameter.

AdaBelief

The authors of AdaBelief introduced the optimizer to:

Converge fast as in adaptive methods.
Have good generalization like SGD.
Be stable during training.

AdaBelief works on the concept of "belief" in the current gradient direction. If it results in good performance, then that direction is trusted, and large updates are applied. Otherwise, it's distrusted and the step size is reduced.

Let's look at a Flax training state that applies the AdaBelief optimizer.

from flax.training import train_state

def create_train_state(rng, learning_rate):
  """Creates initial `TrainState`."""
  cnn = CNN()
  params = cnn.init(rng, jnp.ones([1, size_image, size_image, 3]))['params']
  tx = optax.adabelief(learning_rate)
  return train_state.TrainState.create(
      apply_fn=cnn.apply, params=params, tx=tx)

Here's the performance of AdaBelief on various tasks as provided by its authors.

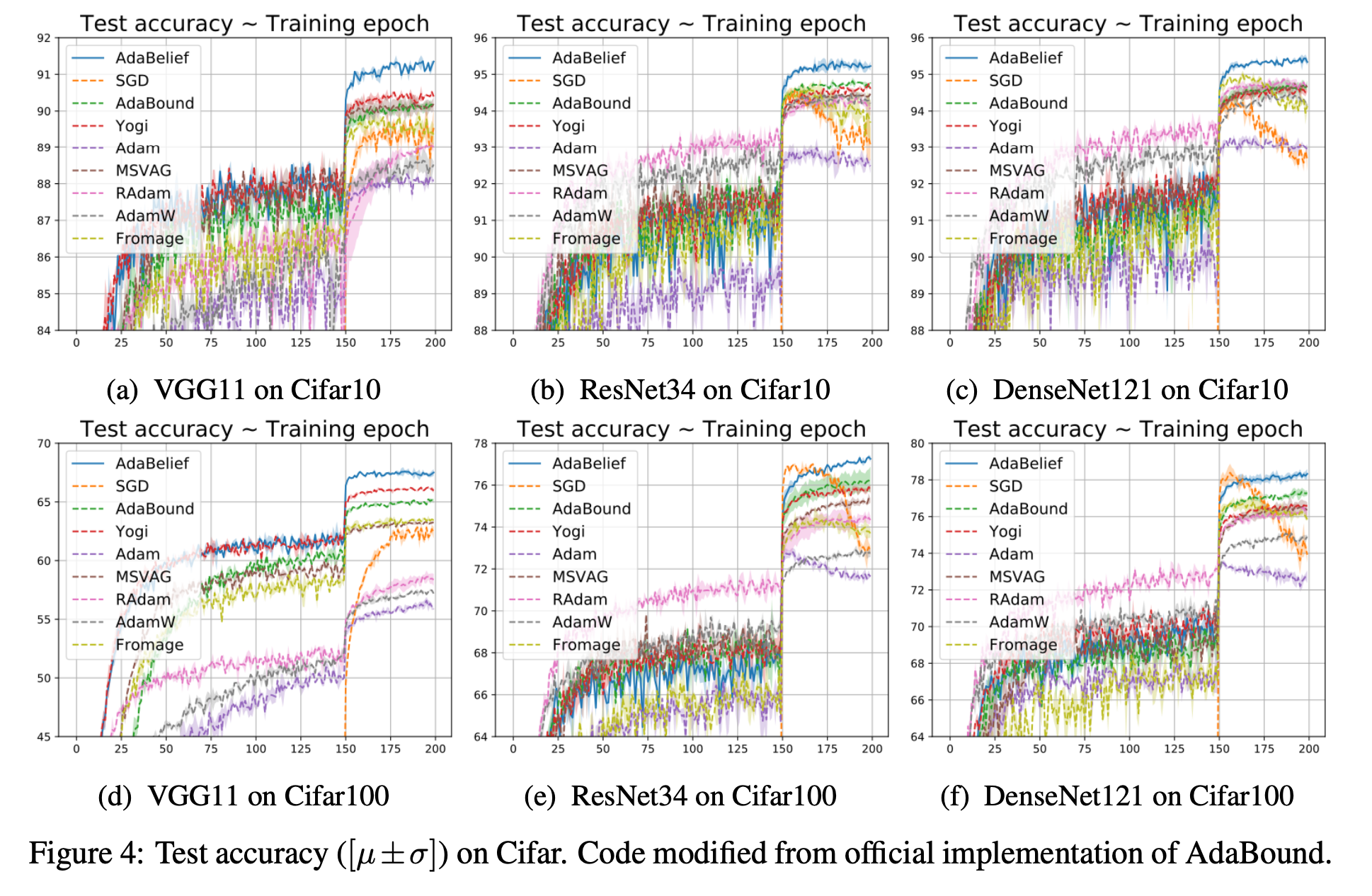
AdaGrad

AdaGrad works well in situations leading to sparse gradients. Adagrad is an algorithm for gradient-based optimization that anneals the learning rate for each parameter during training– Optax.

from flax.training import train_state

def create_train_state(rng, learning_rate):
  """Creates initial `TrainState`."""
  cnn = CNN()
  params = cnn.init(rng, jnp.ones([1, size_image, size_image, 3]))['params']
  tx = optax.AdaGrad(learning_rate)
  return train_state.TrainState.create(
      apply_fn=cnn.apply, params=params, tx=tx)

Adam – Adaptive moment estimation

Adam is a common optimizer in deep learning because it gives good results with default parameters, is computationally inexpensive, and uses little memory.

from flax.training import train_state

def create_train_state(rng):
  """Creates initial `TrainState`."""
  model = LSTMModel()
  params = model.init(rng, jnp.array(X_train_padded[0]))['params']
  tx = optax.adam(0.001,0.9,0.999,1e-07)
  return train_state.TrainState.create(
      apply_fn=model.apply, params=params, tx=tx)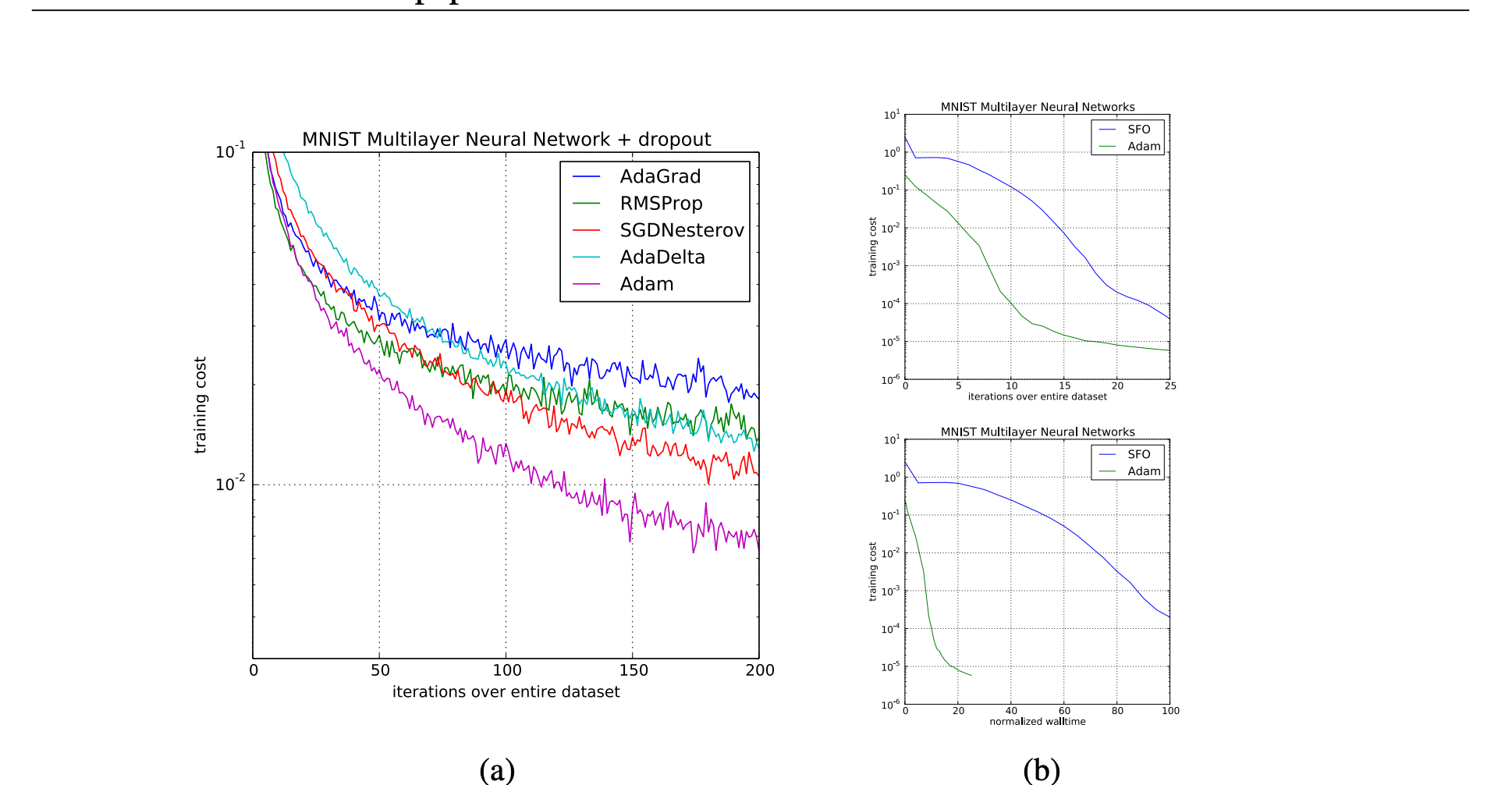

Training of multilayer neural networks on MNIST images. (a) Neural networks using dropout stochastic regularization. (b) Neural networks with deterministic cost function

AdamW

AdamW is Adam with weight decay regularization. Weight decay regularization penalizes the cost function making the weights smaller during backpropagarion. It results in small weights that lead to better generalization. In some cases, Adam with decoupled weight decay leads to better results compared Adam with L2 regularization.

from flax.training import train_state

def create_train_state(rng):
  """Creates initial `TrainState`."""
  model = LSTMModel()
  params = model.init(rng, jnp.array(X_train_padded[0]))['params']
  tx = optax.adamw(0.001,0.9,0.999,1e-07)
  return train_state.TrainState.create(
      apply_fn=model.apply, params=params, tx=tx)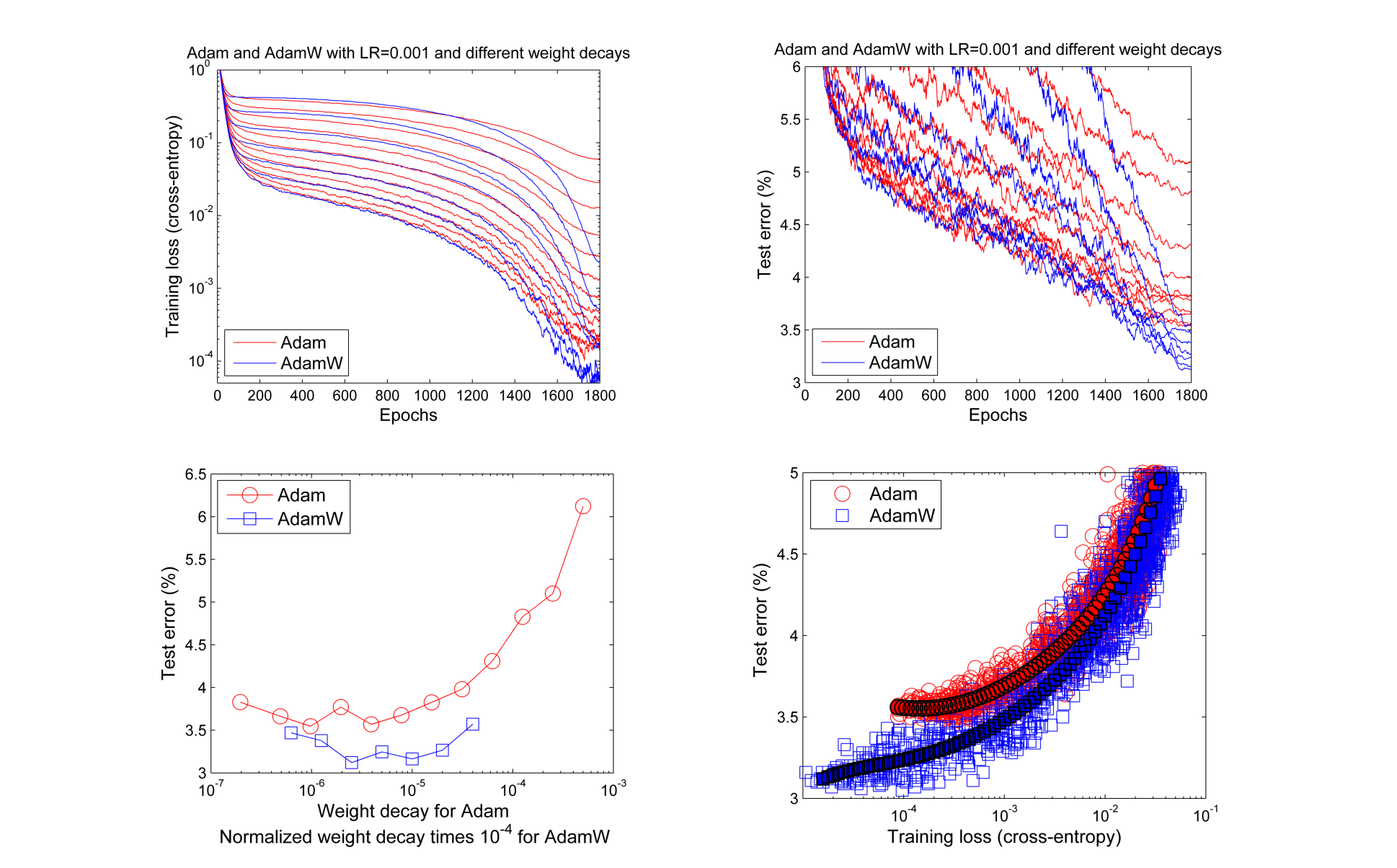

Learning curves (top row) and generalization results (bottom row) obtained by a 26 2x96d ResNet trained with Adam and AdamW on CIFAR-10

RAdam – Rectified Adam optimizer

RAdam aims to solve large variances during the early training stages when applying an adaptive learning rate.

from flax.training import train_state

def create_train_state(rng, learning_rate):
  """Creates initial `TrainState`."""
  cnn = CNN()
  params = cnn.init(rng, jnp.ones([1, size_image, size_image, 3]))['params']
  tx = optax.radam(learning_rate)
  return train_state.TrainState.create(
      apply_fn=cnn.apply, params=params, tx=tx)

AdaFactor

AdaFactor is used for training large neural networks because it is implemented to reduce memory utilization.

from flax.training import train_state

def create_train_state(rng, learning_rate):
  """Creates initial `TrainState`."""
  cnn = CNN()
  params = cnn.init(rng, jnp.ones([1, size_image, size_image, 3]))['params']
  tx = optax.adafactor(learning_rate)
  return train_state.TrainState.create(
      apply_fn=cnn.apply, params=params, tx=tx)

Fromage

Fromage introduces a distance function on deep neural networks called deep relative trust. It requires little to no learning rate tuning.

from flax.training import train_state

def create_train_state(rng, learning_rate):
  """Creates initial `TrainState`."""
  cnn = CNN()
  params = cnn.init(rng, jnp.ones([1, size_image, size_image, 3]))['params']
  tx = optax.fromage(learning_rate)
  return train_state.TrainState.create(
      apply_fn=cnn.apply, params=params, tx=tx)

Lamb – Layerwise adaptive large batch optimization

Lamb aims to enable the training of deep neural networks by computing gradients using large mini-batches. It leads to good performance on attention-based models such as Transformers and ResNet-50.

from flax.training import train_state

def create_train_state(rng, learning_rate):
  """Creates initial `TrainState`."""
  cnn = CNN()
  params = cnn.init(rng, jnp.ones([1, size_image, size_image, 3]))['params']
  tx = optax.lamb(learning_rate)
  return train_state.TrainState.create(
      apply_fn=cnn.apply, params=params, tx=tx)

Lars – Layer-wise Adaptive Rate Scaling

Lars is inspired by Lamb to scale SGD to large batch sizes. Lars has been used to train AlexNet with an 8K batch size and Resnet-50 with a 32K batch size without degrading the accuracy.

from flax.training import train_state

def create_train_state(rng, learning_rate):
  """Creates initial `TrainState`."""
  cnn = CNN()
  params = cnn.init(rng, jnp.ones([1, size_image, size_image, 3]))['params']
  tx = optax.lars(learning_rate)
  return train_state.TrainState.create(
      apply_fn=cnn.apply, params=params, tx=tx)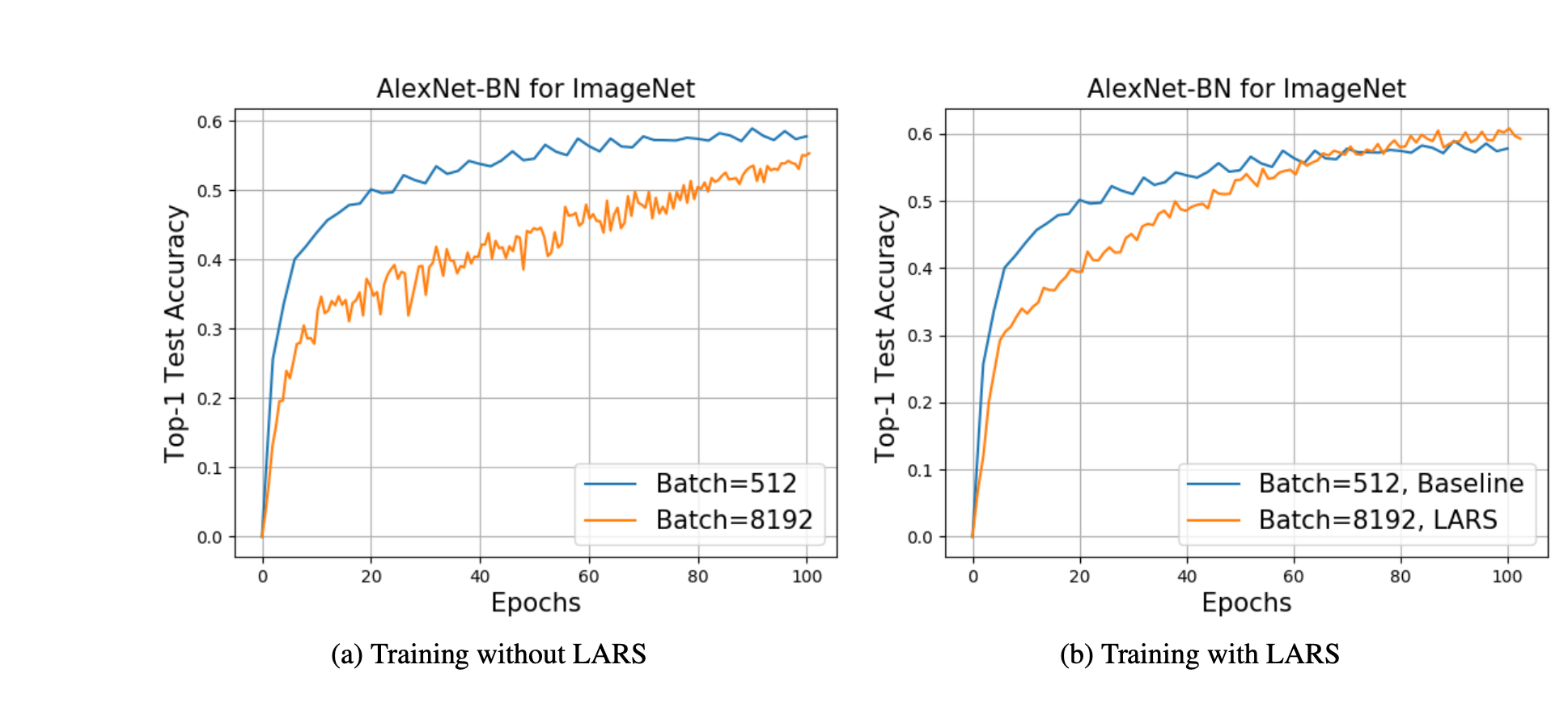

SM3 - Square-root of Minima of Sums of Maxima of Squared-gradients Method

SM3 was designed to reduce memory utilization when training very large models such as Transformer for machine translation, BERT for language modeling, and AmoebaNet-D for image classification

from flax.training import train_state

def create_train_state(rng, learning_rate):
  """Creates initial `TrainState`."""
  cnn = CNN()
  params = cnn.init(rng, jnp.ones([1, size_image, size_image, 3]))['params']
  tx = optax.sm3(learning_rate)
  return train_state.TrainState.create(
      apply_fn=cnn.apply, params=params, tx=tx)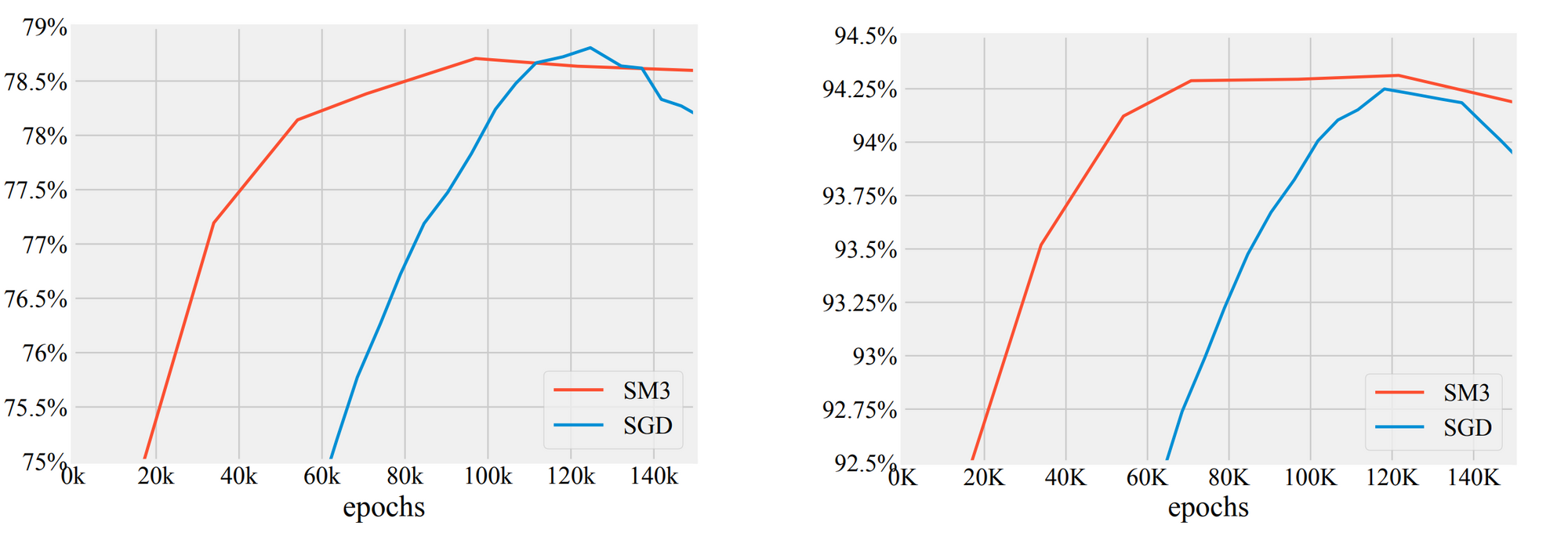

Top-1 (left) and Top-5 (right) test accuracy of AmoebaNet-D on ImageNet

SGD– Stochastic Gradient Descent

SDG implements stochastic gradient descent with support for momentum and Nesterov acceleration. Momentum makes obtaining optimal model weights faster by accelerating gradient descent in a certain direction.

from flax.training import train_state

def create_train_state(rng, learning_rate):
  """Creates initial `TrainState`."""
  cnn = CNN()
  params = cnn.init(rng, jnp.ones([1, size_image, size_image, 3]))['params']
  tx = optax.sgd(learning_rate)
  return train_state.TrainState.create(
      apply_fn=cnn.apply, params=params, tx=tx)

Noisy SGD

Noisy SGD is SGD with added noise. Adding noise to gradients can prevent overfitting and improve training error and generalization in deep architectures.

from flax.training import train_state

def create_train_state(rng, learning_rate):
  """Creates initial `TrainState`."""
  cnn = CNN()
  params = cnn.init(rng, jnp.ones([1, size_image, size_image, 3]))['params']
  tx = optax.noisy_sgd(learning_rate)
  return train_state.TrainState.create(
      apply_fn=cnn.apply, params=params, tx=tx)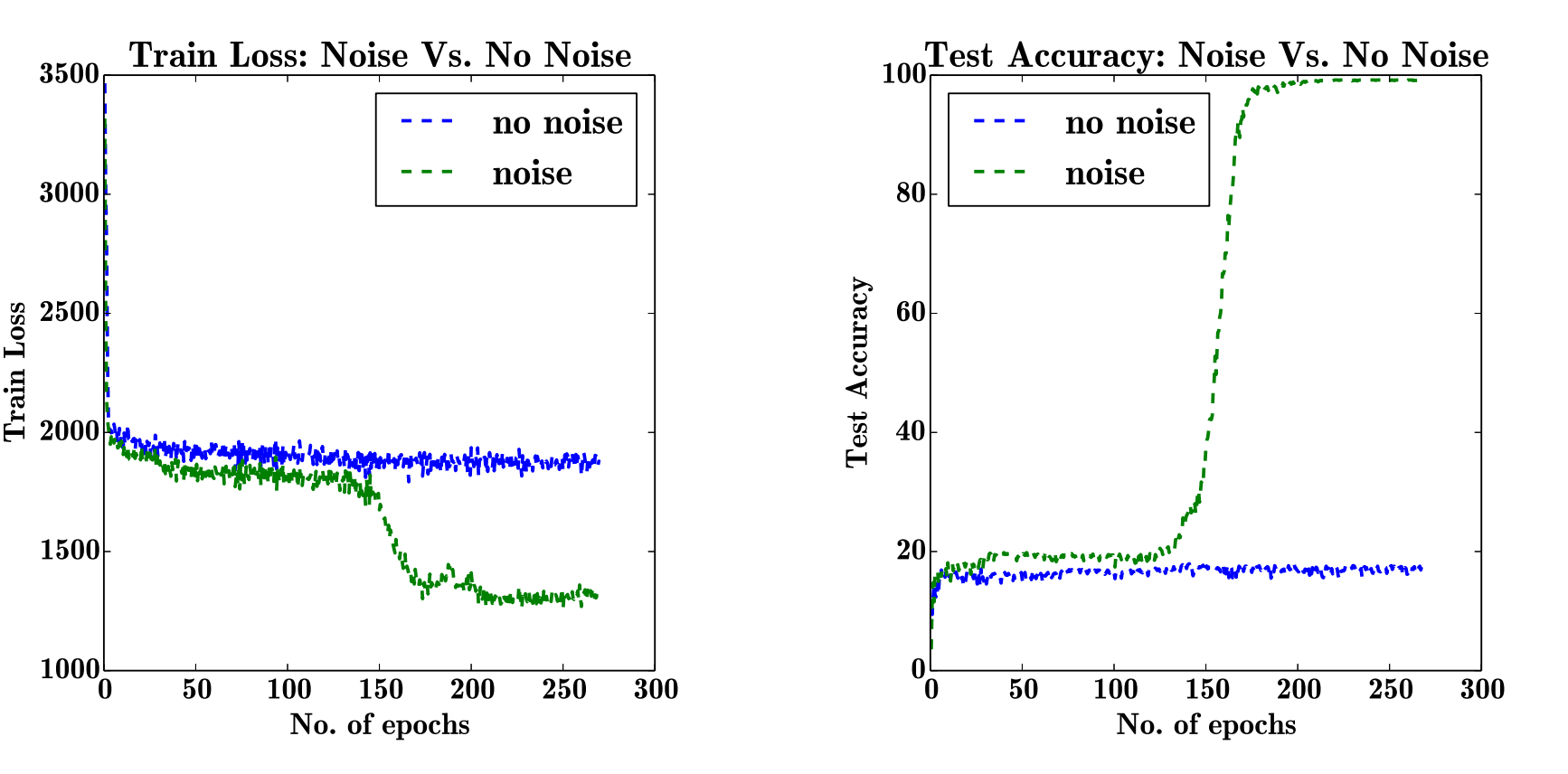

: Noise vs. No Noise in our experiment with tables containing 5 columns. The models trained with noise generalizes almost always better

Optimistic GD

An Optimistic Gradient Descent optimizer.

Optimistic gradient descent is an approximation of extra-gradient methods which require multiple gradient calls to compute the next update. It has strong formal guarantees for last-iterate convergence in min-max games, for which standard gradient descent can oscillate or even diverge– Optax.

from flax.training import train_state

def create_train_state(rng, learning_rate):
  """Creates initial `TrainState`."""
  cnn = CNN()
  params = cnn.init(rng, jnp.ones([1, size_image, size_image, 3]))['params']
  tx = optax.optimistic_gradient_descent(learning_rate)
  return train_state.TrainState.create(
      apply_fn=cnn.apply, params=params, tx=tx)

Differentially Private SGD

Differentially Private SGD is used for training networks with sensitive data. It ensures that the models don't expose sensitive training data.

from flax.training import train_state

def create_train_state(rng, learning_rate):
  """Creates initial `TrainState`."""
  cnn = CNN()
  params = cnn.init(rng, jnp.ones([1, size_image, size_image, 3]))['params']
  tx = optax.dpsgd(learning_rate)
  return train_state.TrainState.create(
      apply_fn=cnn.apply, params=params, tx=tx)

RMSProp

RMSProp works by dividing the gradient of a running average of its recent magnitude–Hinton.

from flax.training import train_state

def create_train_state(rng, learning_rate):
  """Creates initial `TrainState`."""
  cnn = CNN()
  params = cnn.init(rng, jnp.ones([1, size_image, size_image, 3]))['params']
  tx = optax.rmsprop(learning_rate)
  return train_state.TrainState.create(
      apply_fn=cnn.apply, params=params, tx=tx)

Yogi

Yogi is a modified Adam optimizer for optimizing the stochastic nonconvex optimization problem.

from flax.training import train_state

def create_train_state(rng, learning_rate):
  """Creates initial `TrainState`."""
  cnn = CNN()
  params = cnn.init(rng, jnp.ones([1, size_image, size_image, 3]))['params']
  tx = optax.yogi(learning_rate)
  return train_state.TrainState.create(
      apply_fn=cnn.apply, params=params, tx=tx)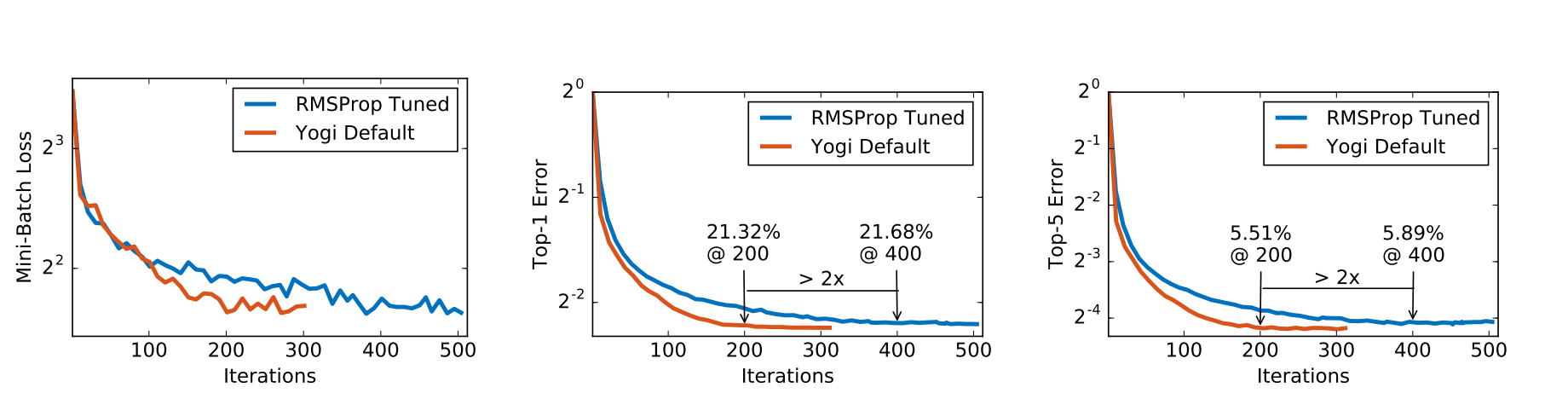

Comparison of highly tuned RMSProp optimizer with YOGI for Inception-Resnet-v2 on Imagenet. First plot shows the mini-batch estimate of the loss during training, while the remaining two plots show top-1 and top-5 error rates on the held-out Imagenet validation set

Final thoughts

Choosing the right optimizer function determines how long training a network will take. It also determines how well the model performs. Choosing the appropriate optimizer functions is therefore paramount. This article discusses various optimizer functions that you can apply to your JAX and Flax networks. In particular, you walk away with nuggets about these optimizers:

Adam optimizer in JAX.
RMSProp optimizer in Flax.
Stochastic Gradient Descent in JAX.

..to mention a few.