Activation functions in JAX and Flax

Activation functions are applied in neural networks to ensure that the network outputs the desired result. The activations functions cap the output within a specific range. For instance, when solving a binary classification problem, the outcome should be a number between 0 and 1. This indicates the probability of an item belonging to either of the two classes. However, in a regression problem, you want the numerical prediction of a quantity, for example, the price of an item. You should, therefore, choose an appropriate activation function for the problem being solved.

Let's look at common activation functions in JAX and Flax.

ReLU – Rectified linear unit

The ReLU activation function is primarily used in the hidden layers of neural networks to ensure non-linearity. The function caps all outputs to zero and above. Outputs below zero are returned as zero, while numbers above zero are returned as they are. This ensures that there are no negative numbers in the network.

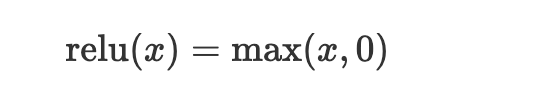
On line 9 we apply the ReLu activation function after the convolution layer.

import flax
from flax import linen as nn  

class CNN(nn.Module):

  @nn.compact
  def __call__(self, x):
    x = nn.Conv(features=32, kernel_size=(3, 3))(x)
    x = nn.relu(x)
    x = nn.avg_pool(x, window_shape=(2, 2), strides=(2, 2))
    x = nn.Conv(features=64, kernel_size=(3, 3))(x)
    x = nn.relu(x)
    x = nn.avg_pool(x, window_shape=(2, 2), strides=(2, 2))
    x = x.reshape((x.shape[0], -1))  
    x = nn.Dense(features=256)(x)
    x = nn.relu(x)
    x = nn.Dense(features=2)(x)
    x = nn.log_softmax(x)
    return x

PReLU– Parametric Rectified Linear Unit

Parametric Rectified Linear Unit is ReLU with extra parameters equal to the number of channels. It works by introducing a– a learnable parameter. PReLU allows for non-negative values.

x = nn.PReLU(x)

Sigmoid

The sigmoid activation function caps output to a number between 0 and 1 and is mainly used for binary classification tasks. Sigmoid is used where the classes are non-exclusive. For example, an image can have a car, a building, a tree, etc. Just because there is a car in the image doesn’t mean a tree can’t be in the picture. Use the sigmoid function when there is more than one correct answer.

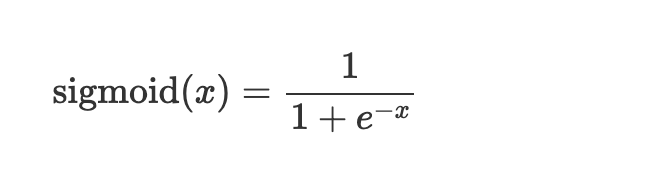
x = nn.sigmoid(x)

Log sigmoid

Log sigmoid computes the log of the sigmoid activation, and its output is within the range of −∞ to 0.

x = nn.log_sigmoid(x)

Softmax

The softmax activation function is a variant of the sigmoid function used in multi-class problems where labels are mutually exclusive. For example, a picture is either grayscale or color. Use the softmax activation when there is only one correct answer.

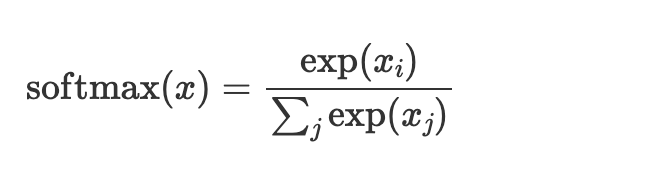
x = nn.softmax(x)

Log softmax

Log softmax computes the logarithm of the softmax function, which rescales elements to the range −∞ to 0.

x = nn.log_softmax(x)

ELU – Exponential linear unit activation

ELU activation function helps in solving the vanishing and exploding gradients problem. Unlike ReLu, ELU allows negative numbers pushing the mean unit activations closer to zero. ELUs may lead to faster training and better generalization in networks with more than five layers.

For values above zero the number is returned as is but for numbers below zeros they are a number that is less that but close to zero.

x = nn.elu(x)

CELU – Continuously-differentiable exponential linear unit

CELU is ELU that is continuously differentiable.

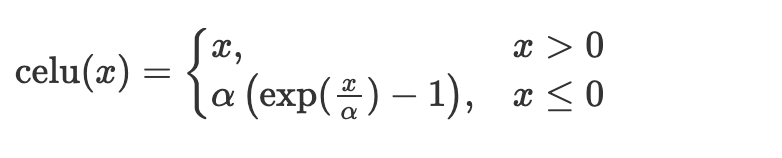
x = nn.celu(x)

GELU– Gaussian error linear unit activation

GELU non-linearity weights inputs by their value rather than gates inputs by their sign as in ReLU– Source.

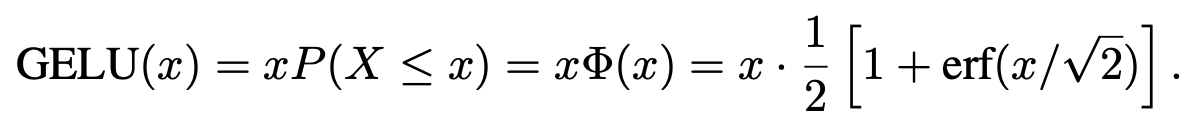
x = nn.gelu(x)

GLU – Gated linear unit activation

GLU is computed as GLU(a,b)=a⊗σ(b). It has been applied in Gated CNNs for natural language processing. In the formula, the b gate controls what information is passed to the next layer. GLU helps tackle the vanishing gradient problem.

x = nn.glu(x)

Soft sign

The Soft sign activation function caps values between -1 and 1. It is similar to the hyperbolic tangent activation function– tanh. The difference is that tanh converges exponentially while Soft sign converges polynomially.

x = nn.soft_sign(x)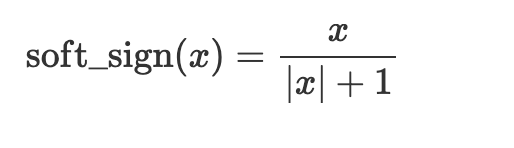

Softplus

The Softplus activation returns values as zero and above. It is a smooth version of the ReLu.

x = nn.soft_plus(x)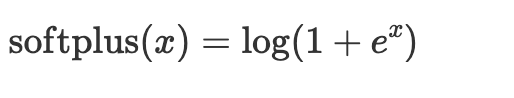

Swish–Sigmoid Linear Unit( SiLU)

The SiLU activation function is computed as x * sigmoid(beta * x) where beta is the hyperparameter for Swish activation function. SiLU, is, therefore, computed by multiplying the sigmoid function with its input.

x = nn.swish(x)

Custom activation functions in JAX and Flax

You can also define custom activation functions in JAX. For example, here's how you'd define the LeakyReLu activation function.

from flax import linen as nn  
import jax.numpy as jnp

class LeakyReLU(nn.Module):
    alpha : float = 0.1

    def __call__(self, x):
        return jnp.where(x > 0, x, self.alpha * x)

Final thoughts

You have learned about the various activation functions you can use in JAX and Flax. You have also seen that you can create new functions by creating a class that implements the __call__ method.

Want to dive deeper into JAX and Flax? Here are some more resources from our blog:

• What is JAX?
• Flax vs. TensorFlow
• JAX loss functions
• Optimizers in JAX and Flax
• How to load datasets in JAX using TensorFlow
• Building Convolutional Neural Networks in JAX and Flax
• Distributed training in JAX
• Using TensorBoard in JAX and Flax
• LSTM in JAX & Flax
• Elegy (High-level API for deep learning in JAX & Flax)

Follow us on LinkedIn, Twitter, GitHub, and subscribe to our blog, so you don't miss a new issue.